The sound produced by a vibrating string is complex. This was described in the 18th c. by Swiss mathematicians Daniel Bernoulli and Leonhard Euler as the ‘superposition of the fundamental and harmonic vibrations’.[1] Strictly speaking this description is incorrect. In theory a perfectly elastic string would generate upper partials that are in tune with the harmonic series but because real strings must have some stiffness, the upper partials of a string tone are always slightly sharp, and progressively sharp.
This is the phenomenon known as inharmonicity. While the term might seem to imply discord, it is in fact what gives string tones their warmth and character. The slight rise in their upper partials leads to a stretching of the octave that the human ear seems to expect or prefer and instruments tuned in this manner are often referred to as more ‘alive’.
As mentioned elsewhere under optimum tension, the limit on the size of the safety factor according to modern writers is ‘three semitones below breaking point’ or less. In A History of the Harpsichord Edward Kottick points out that when tuned below this limit strings begin to sound ‘false’.[2] This poor quality of tone will be largely due to increased inharmonicity resulting from the lower tensioning of the strings.
Of course, tone quality is a matter of individual taste and determining what sounds good and what does not will always be somewhat subjective, but inharmonicity is a quantifiable aspect of the sound produced by vibrating strings and ultimately their tone quality. Inharmonicity is the measure of the amount by which the upper partials of a string tone are sharp or ‘out of tune’. With reduced tension the upper partials become progressively sharper, more and more out of tune.
Many other factors contribute to the qualities of a string tone but inharmonicity has an influence on the perception of intervals[3] and will affect the harper’s ability tune and temper the instrument, as such it is a crucially important aspect of the sound of a harp string.
Studies have shown that in the tuning of intervals the ear relies mostly on a mechanism known as ‘partial matching’. Meaning that the ear will try to match the harmonic spectrum of one tone with that of the other. For example, when tuning an octave on the harp the ear will try to match the second partial (first above the fundamental) of the lower tone with the first partial (fundamental) of the upper one and so on.
Where inharmonicity is reasonably low or rises gently this leads to a slight stretching of the octave that sounds natural and pleasing. But problems will arise and fine–tuning will become difficult when inharmonicity is too high or fluctuates throughout the compass.
On an instrument such as the metal–strung harp where each note and the harmonics it excites in the other strings will continue ringing unless they are damped this can become very frustrating, particularly in tuning the lower range where the amplitude of these partials is generally greater. So it would appear that in designing and stringing a harp it would be desirable if not imperative that inharmonicity should be kept to a minimum.
Inharmonicity is a function of the proportions of a string, the elasticity and density of the string material, and tension. The partials deviate from the fundamental frequency ƒ according to the following equation:[4]
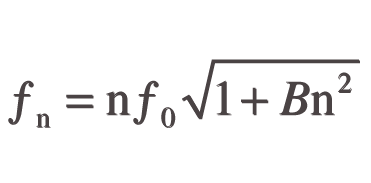
Where here n is the partial number B is the basic coefficient of inharmonicity (in Hertz), which can be expressed with the following equation:[5]
B = (π/8)2(Q/ρ)(d/ƒl2)2
Where:
Q = Young’s modulus in dn
ρ = Density of the material in g/cm3
d = Diameter in cm
ƒ = Frequency in Hz
l = Length in cm
The first factor in the equation (π/8)2 is a constant, 0.154213.
The second factor (Q/ρ) confirms what many modern players have found in practice i.e. greater elasticity (smaller values for Young’s Modulus indicate greater elasticity) and density result in lower inharmonicity.
In recent years many harpers have improved the tone of their instruments by using precious metal strings in the bass register. Silver has a greater density and elasticity than any copper–based alloy and gold even more so. Typical values for copper–based alloys would be ρ = 8.8 g/cm3 and Q = 110 GPa, sterling silver ρ = 10.4 g/cm3 and Q = 75 GPa and ρ = 15 g/cm3 and Q = 75 GPa for 18 carat gold.
The third factor (d/ƒl2)2 expresses the following axiom: thinner and longer strings at higher frequencies (at a higher tension) will have a lower coefficient of inharmonicity, confirming the observation made by early writers that ‘strings sound their best at higher tensions’. Inharmonicity in plain piano strings is a well–documented phenomenon and much has been written on the subject since the 1950s. In an article entitled ‘String Inharmonicity and Piano Tuning’ the authors state that:
‘Values [for the coefficient of inharmonicity] between 0.0001[0.086] and 0.001[0.865] have small but discernable effects. Values greater than 0.001[0.865] significantly change partial frequencies and beat frequencies and affect tuning practice…The tones of harpsichord strings, being longer and thinner than piano strings, have, as a rule, inharmonicities that stay under 0.0005 [0.432] and can be neglected in the tuning process.’ [6]
While some members of the harpsichord fraternity might not agree with the last portion of this statement, these values may be taken as a guideline for what might be termed ‘manageable’ levels of inharmonicity. It should be remembered however that as the fundamental frequencies rise in pitch so the do their partials and at some point the partials of higher tones become barely audible so their effect on tuning would be negligible. For example the harmonic frequency of the fourth partial of a 110 Hz (A) tone would be 440 Hz, well within the audible range, whereas the fourth partial of a 880 Hz tone would be 3520 Hz. While it is still in the audible range, barely, this frequency is higher than the highest note on the average harp. Higher inharmonicity values here would be of no great consequence as regards tuning.
Unless extremely thin strings are used for the highest octave on the harp the coefficient of inharmonicity will rise dramatically towards the highest string with values much higher than 0.001[0.865]. Clearly, changing the proportions of a string by using a thinner gauge could redress any problems that might arise as a result of a relatively high coefficient of inharmonicity. However, there will come a point when the string will begin to feel weak and floppy.
Finally, it should be pointed out that when estimating partial frequencies for any given string one should bear in mind the fact the amplitude of the partials decreases as their number increases. In other words one should not be too alarmed to find that the 16th partial of a string tone could deviate from its ‘harmonic’ frequency by as much as 250 cents and more as this partial will not be audible. Not very much can ever really be heard beyond the first eight partials, with the second taking precedence over the others then the third and so on.
[1] These harmonic vibrations are also known as overtones or partials. A partial describes any one of the vibrations or frequencies that forms part of the complex (sound) including the fundamental, and an overtone describes any partial above the fundamental frequency.
[2] Edward L. Kottick, A History of the Harpsichord, (Bloomington: Indiana University Press, 2003), 16. This may be true of harpsichord strings as they are comparatively long and thin and generate upper partials with greater amplitude than strings of shorter proportions, making increased inharmonicity more noticeable. There may well be more leeway on this three–semitone limit for other instruments.
[3] See Elisabeth A. Cohen, ‘Some Effects of Inharmonic Partials on Interval Perception’, Music Perception, I/3, (1984), 323–349.
[4] R. W. Young, ‘Inharmonicity of Plain Wire PianoStrings’, Journal of the Acoustical Society of America Vol.24, no 3, (1952). Equivalent to Eq. 6.
[5] Rewritten from Young (1952) Eq. 6. See Rudlof A. Rasch and Vincent Heetvelt, ‘String Inharmonicity and Piano Tuning’, Music Perception, III/2, (1985), 171–190, at 175. See also About notes 4 and 5.
[6] Rasch (1985), 174–5. The values in [square brackets] have been multiplied by the 865.62 conversion factor for comparison purposes. A number authors use a coefficient of inharmonicity equivalent to B*865.62 to calculate inharmonicity in cents (see p.176). See also About.
Submitted by Paul Dooley, 21 March, 2013. © 2004-2013 Paul Dooley
Except where otherwise noted, content on this site is licensed under a Creative Commons License.
Permissions beyond the scope of this license may be available by contacting us at editor@wirestrungharp.com.
