The amount of elastic potential energy (EPE) stored in a string is given by the following equation
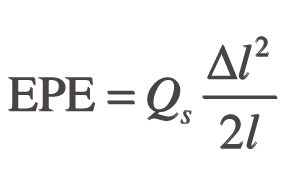
Where Δl is the extension resulting from the tensioning of the string and the plucking action, l is the natural length of the string and Qs is the net elasticity or ‘relative strength’ of the wire
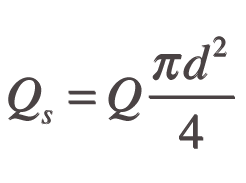
Where
Q = Young's modulus
d = diameter
To calculate the amount of energy stored in a harp string with its known parameters when under tension the natural length l of the string must be established first in order to calculate the elongation Δl.
Let
Δl1 = the elongation resulting from the initial string tension
Δl2 = the elongation resulting from the plucking action
Δl = ??Δl1+Δl2 = total elongation
l = the natural length of the string
l1 = the vibrating length of the string under tension
From Hooke’s Law
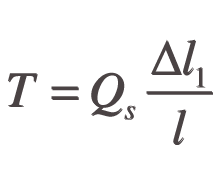
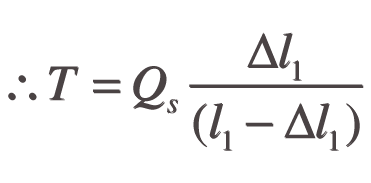
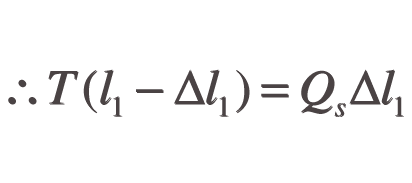
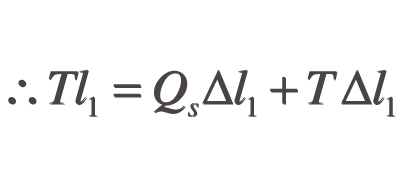
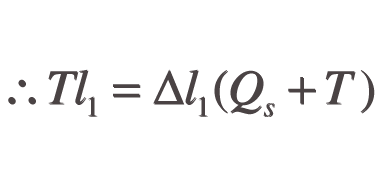
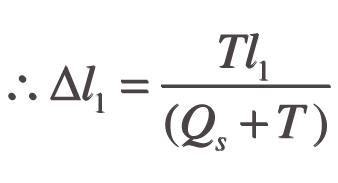
Values for Qs (Q and d), l1 and T are known for any given string, allowing Δl1 to be calculated and therefore l, which is equal to l1-Δl1
The elongation resulting from the plucking action Δl2 can be calculated thus
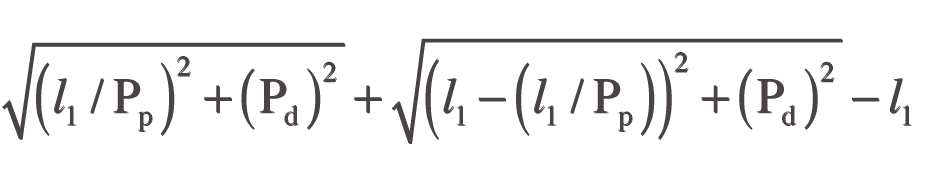
Where Pp is the plucking point and Pd is the plucking depth.
Submitted by Paul Dooley, 21 March, 2013. © 2004-2013 Paul Dooley
Except where otherwise noted, content on this site is licensed under a Creative Commons License.
Permissions beyond the scope of this license may be available by contacting us at editor@wirestrungharp.com.
